Intorno al 1780 Alessandro Volta, nell’ambito dei suoi studi sull’elettricità, nota che lo scudo carico di un elettroforo perpetuo, appoggiato sulla superficie di alcuni materiali scarsamente conduttori, anziché dissipare la propria elettricità la conserva meglio che isolato in aria. Si convinse che l’afflusso di carica sulla superficie prossima a quella dello scudo richiama carica sulla superficie affacciata di quest’ultimo. Due dischi metallici, delle stesse dimensioni, così che uno può essere sovrapposto all’altro in modo da combaciare perfettamente, compongono quello che Volta stesso chiama “condensatore di elettricità”.

Un condensatore (indicato abitualmente con C) è generalmente costituito da una coppia di conduttori (armature o piastre) separati da un isolante (dielettrico). La carica è immagazzinata sulla superficie delle piastre, sul bordo a contatto con il dielettrico. Quindi all’esterno si avrà un campo elettrico pari a zero a causa dei due campi, uno positivo e uno negativo, che hanno per l’appunto stesso modulo ma segno (verso) opposto, mentre all’interno del dispositivo due volte il campo elettrico perché entrambi i campi, sia quello positivo sia quello negativo, hanno stesso modulo e stesso verso. L’energia elettrostatica che il condensatore accumula si localizza nel materiale dielettrico che è interposto fra le armature.

La capacità (in un condensatore lineare)Modifica

Lo stesso argomento in dettaglio: Capacità elettrica.

Struttura di un condensatore

Se si applica una tensione elettrica alle armature, le cariche elettriche si separano e si genera un campo elettrico all’interno del dielettrico. L’armatura collegata al potenzialepiù alto si carica positivamente, negativamente l’altra. Le cariche positive e negative sono uguali e il loro valore assoluto costituisce la carica Q del condensatore. La carica è proporzionale alla tensione applicata e la costante di proporzionalità è una caratteristica di quel particolare condensatore che si chiama capacità elettrica e si misura in farad:

${\displaystyle C={\frac {Q}{\Delta V}}}$

Ossia la capacità è uguale al rapporto tra la carica elettrica fornita Q e la tensione elettrica applicata ΔV. La capacità di un condensatore piano (armature piane e parallele) è proporzionale al rapporto tra la superficie S di una delle armature e la loro distanza d. La costante di proporzionalità è una caratteristica dell’isolante interposto e si chiama permittività elettrica assoluta e si misura in farad/m.

La capacità di un condensatore piano a facce parallele è quindi:

${\displaystyle C=\ S{\frac {\varepsilon }{d}}}$

In figura non sono rappresentati i cosiddetti effetti di bordo ai confini delle facce parallele dove le linee di forza del campo elettrico da una faccia all’altra non sono più rettilinee ma via via più curve.

L’energiaModifica

L’energia immagazzinata in un condensatore è pari al lavoro fatto per caricarlo. Si consideri, ora, un condensatore con capacità C, con carica +q su una piastra e –q sull’altra. Per muovere un piccolo elemento di carica dq da una piastra all’altra sotto l’azione della differenza di potenziale V=q/C, il lavoro necessario è dW:

${\displaystyle \operatorname {d} W=V\operatorname {d} q={\frac {q}{C}}\,\operatorname {d} q}$

Integrando questa equazione, infine, si può determinare l’energia potenziale Uimmagazzinata dal condensatore. Gli estremi dell’integrazione saranno 0, ovvero un condensatore scarico, e Q, ovvero la carica immessa sui piatti del condensatore:

${\displaystyle W=\int _{0}^{Q}{\frac {q}{C}}\,\operatorname {d} q={\frac {1}{2}}{\frac {Q^{2}}{C}}={\frac {1}{2}}C\,V^{2}=U}$

Forze sulle armature e sul dielettricoModifica

Le due piastre del condensatore sono caricate con cariche di segno opposto, quindi esiste un campo elettrico E fra le piastre. Tale campo E istante per istante è direttamente proporzionale all’energia U che si trova nel condensatore e inversamente proporzionale alla distanza d fra le piastre.

${\displaystyle |{\vec {E}}|={\frac {U}{d}}}$

Questo risultato vale sia nel caso in cui il condensatore sia collegato a un circuito esterno che mantenga costante la tensione fra le piastre, che nel caso in cui il condensatore sia isolato e sia costante la carica sulle piastre.

La capacità di un condensatore aumenta se fra le piastre viene inserito un dielettrico con una buona costante dielettrica. In tal caso, se il condensatore è isolato e la carica rimane costante, l’energia immagazzinata nel condensatore scende e questa energia fornisce il lavoro necessario per “risucchiare” il dielettrico dentro il condensatore. Una lastra di dielettrico che si inserisce esattamente nello spazio tra le piastre viene risucchiata con una forza F non costante che dipende dalla lunghezza x della porzione di lastra già entrata fra le piastre. È facile dimostrare che tale forza è:

${\displaystyle F={\frac {U_{0}}{\ell }}{\frac {\varepsilon _{r}-1}{[1+(x/\ell )(\varepsilon _{r}-1)]^{2}}}}$

Dove

è la costante dielettrica relativa della lastra,

è l’energia nel condensatore all’inizio dell’inserzione (

) e

è la corsa del dielettrico (ovvero per

il dielettrico è completamente inserito). La situazione cambia se il dielettrico è inserito mentre il condensatore è collegato a un circuito che mantenga costante la tensione tra le piastre. In tal caso la forza di risucchio rimane costante e non dipende da x e vale:

${\displaystyle F={\frac {U_{0}(\varepsilon _{r}-1)}{\ell }}}$

Lo stesso argomento in dettaglio: Circuito elettrico.

Il condensatore è un componente di grande importanza e utilizzo all’interno dei circuiti elettrici. Nel seguito si espone il suo comportamento sia in corrente continua sia in corrente alternata.

Equazione caratteristicaModifica

Dal momento che gli elettroni non possono passare direttamente da una piastra all’altra attraverso il dielettrico che le separa, il condensatore costituisce una discontinuità elettrica nel circuito: quando viene applicata una differenza di potenziale a un condensatore utilizzando un generatore, le due armature si caricano di una quantità Quguale in modulo, ma di segno opposto indotta da un’armatura all’altra. Se la differenza di potenziale è variabile nel tempo si produce inoltre una corrente virtuale indotta, detta corrente di spostamento. Nel dielettrico si assiste al fenomeno della polarizzazione: le molecole si dispongono a formare un dipolo elettrico.
Sapendo che la differenza di potenziale tra le armature è direttamente proporzionale alla carica accumulata su di esse e inversamente proporzionale alla capacità del dispositivo, si ottiene che l’espressione per la tensione è:

${\displaystyle v(t)={\frac {q(t)}{C}}={\frac {1}{C}}\int _{t_{0}}^{t}i(\tau )\mathrm {d} \tau +v(t_{0})}$

.

prendendo la derivata e moltiplicando per la capacità C si ottiene l’espressione per la corrente:

${\displaystyle i(t)={\frac {\mathrm {d} q(t)}{\mathrm {d} t}}=C{\frac {\mathrm {d} v(t)}{\mathrm {d} t}}}$

.

Questa formula equivale alla definizione fisica di corrente di spostamento scritta in termini di potenziale variabile nel tempo anziché in termini di campo elettrico variabile nel tempo. Le due precedenti espressioni costituiscono le relazioni costituitive del condensatore in un circuito elettrico.

Se scriviamo

come

, valida per un condensatore piano, si nota che il campo

indotto sulle facce del condensatore diminuisce all’aumentare della distanza

tra le armature, e quindi è inversamente proporzionale alla capacità elettrica

: la capacità indica quindi un accumulo di energia elettrica nel condensatore stesso.

Funzionamento in serie e in paralleloModifica

Lo stesso argomento in dettaglio: Circuiti in serie e in parallelo.

Condensatori in parallelo

Condensatori in serie

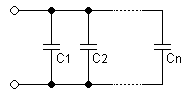
Quando si montano n condensatori in parallelo su ognuno di essi si misurerà la medesima caduta di potenziale. La capacità equivalente

sarà, quindi, data dalla formula:

${\displaystyle C_{eq}=\sum _{i=1}^{n}C_{i}=C_{1}+C_{2}+\cdots +C_{n}}$

Quando si montano n condensatori in serie, attraverso ognuno di essi passerà la stessa carica istantanea (in regime dinamico, la stessa corrente), mentre la caduta di potenziale sarà differente da condensatore a condensatore; in particolare, essendo

, a parità di Q la tensione maggiore sarà localizzata ai morsetti della capacità minore. La capacità equivalente totale

sarà pertanto definita dalla seguente relazione:

${\displaystyle {\frac {1}{C_{eq}}}=\sum _{i=1}^{n}{\frac {1}{C}}_{i}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\cdots +{\frac {1}{C_{n}}}}$

Comportamento in regime costante